Paper reading | Tìm hiểu mô hình ResNeXt

Đóng góp của bài báo

Bài báo giới thiệu một kiến trúc mô hình mới có tên ResNeXt (Residual Next) là phiên bản nâng cấp từ ResNet. ResNeXt đạt vị trí thứ 2 trong ILSVRC 2016 classification task (xem hình dưới) với top 5 error rate khoảng 3.03%. So sánh với ResNet (vô địch ILSVRC 2015 với top 5 error rate là 3.57%) và PolyNet (đứng thứ 2 với 3.04%), ResNeXt có hiệu suất tốt hơn khoảng 15%, một con số khá ấn tượng

ResNeXt giới thiệu "cardinality block", đây là một phần mới được thêm vào trong kiến trúc mạng ResNeXt. Cardinality block có nhiệm vụ tạo ra sự phân chia (split) của các kênh đầu vào thành nhiều "nhóm cardinality" (cardinality groups). Mỗi nhóm cardinality đại diện cho một tập hợp các đặc trưng (features) cụ thể mà mạng sẽ học.

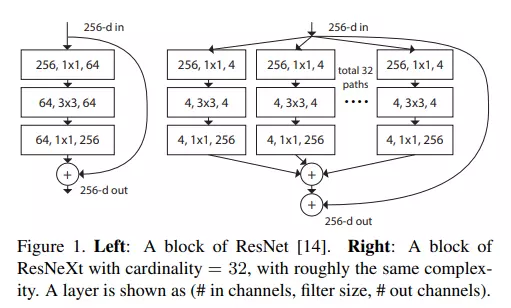
Ta có thể hiểu rằng khi dữ liệu được đưa vào mạng, các kênh (channels) của dữ liệu đó được chia thành nhiều phần nhỏ hơn (những nhóm cardinality). Điều này tạo ra một khả năng học đồng thời nhiều loại đặc trưng khác nhau từ dữ liệu đầu vào. Các nhóm cardinality này hoạt động độc lập với nhau. Mỗi nhóm sẽ học những đặc trưng riêng của nó từ dữ liệu. Điều này cho phép mô hình học được nhiều loại thông tin đa dạng từ dữ liệu đầu vào. Sau khi mỗi nhóm cardinality đã học được những đặc trưng của riêng, các đặc trưng này sẽ được kết hợp (integrated) lại để tạo ra đầu ra cuối cùng (chiến lược split-transform-merge). Quá trình tích hợp này thường là sự tổng hợp có trọng số (weighted total), có nghĩa là mỗi nhóm cardinality đóng góp một phần trong việc tạo ra đầu ra cuối cùng của mô hình.

Phương pháp

Nhắc lại cách tổng hợp neuron trong ANN

Mô hình ResNeXt có ý tưởng cơ bản giống như cách tổng hợp neuron trong ANN với chiến lược split-transform-merge (trong bài báo ghi là splitting, transforming và aggregating ).

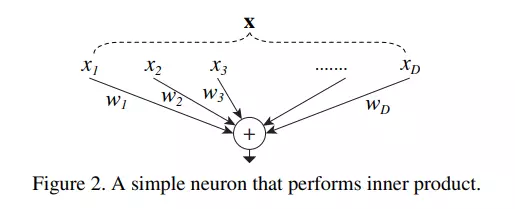
Splitting thể hiện ở việc vector $x$ ban đầu được cắt thành các low-dimensional embedding với các không gian con đơn chiều (single-dimension) $x_i$ . Transforming: Các biểu diễn low-dimensional được biến đổi, hay được scale $w_i x_i$ . Aggregating: Các biến đổi trong tất cả các embedding được tổng hợp theo công thức $\sum_{i=1}^D$ .

Aggregated Transformations

Tương tự ý tưởng tổng hợp neuron được trình bày trong phần vừa rồi, mô hình ResNeXt được xây dựng theo hướng "Network-in-Neuron". Thay vì tổng hợp tuyến tính tại mỗi path như neuron, mô hình ResNeXt sử dụng các function phi tuyến tính trên mỗi path.

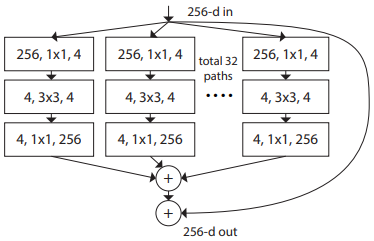
Ta có thể biểu diễn giai đoạn Transformation này theo công thức như sau:

$\mathcal{F}(\mathbf{x})=\sum_{i=1}^C \mathcal{T}_i(\mathbf{x})$

trong đó $\mathcal{T}_i(\mathbf{x})$ là một hàm bất kì. Nếu so sánh với neuron thì đây chính là $x$ . $C$ là cardinality. $C$ ở đây giống như $D$ trong phương trình tổng hợp neuron. $C$ không nhất thiết phải bằng $D$ và có thể mang giá trị bất kì. Giá trị $C$ này kiểm soát độ phức tạp của giai đoạn transformation. Tất cả $\mathcal{T}_i(\mathbf{x})$ đều có topology giống nhau.

Mối quan hệ giữa Inception-ResNet và Group Convolution trong ResNeXt

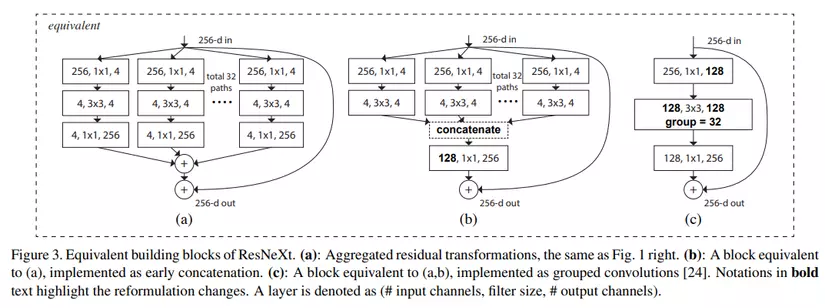
Hình trên là các block khác nhau lần lượt là ResNeXt Block, Inception-ResNet Block và Grouped Convolution. 3 block này đều có cùng dimension input và dimension output. Ta sẽ cùng đi phân tích và so sánh các block này.

Với ResNeXt block, các path độc lập với nhau và mỗi path bao gồm 3 Conv là Conv1×1, Conv3×3 và Conv1×1. Internal dimension của mỗi path là $d=4$ . Cardinality có giá trị $C=32$ . Nếu như tổng hợp tất cả dimension của Conv3x3, ta sẽ có số dimension là $d \times C = 4 \times 32 = 128$ . Nhận thấy rằng, dimension được tăng trực tiếp từ 4 đến 256 và sau đó các path được cộng với nhau, kết quả lại tiếp tục được cộng với đầu vào ban đầu thông qua một skip connection path. So sánh với Inception-ResNet block, ta thấy rằng dimension của Inception-ResNet block tăng dần từ 4 tới 128 rồi mới đến 256, vì vậy ta có thể nhận xét rằng, việc thiết kế ResNeXt path đơn giản hơn so với Inception-ResNet.

Với Inception-ResNet block, mỗi path gồm 2 Conv là Conv1×1 và Conv3×3. Sau đó, các feature tại mỗi path được concat với nhau cho ra feature mới có dimension là 128. Feature này tiếp tục đi qua Conv1x1 và tiếp tục cho ra feature mới có dimension là 256. Cuối cùng, feature output này được cộng với input thông qua một skip connection path. So với ResNeXt block, ta sử dụng phép concat sớm sau Conv thứ 2 (Conv3x3).

Đối với Grouped Convolution, ta sử dụng một kiến trúc đơn giản hơn gồm duy nhất 1 path (Conv1×1–Conv3×3–Conv1×1). Layer grouped convolution là conv3x3 nhưng "rộng hơn", tức là có nhiều kernel và các neuron kết nối thưa với nhau. Ở đây Layer grouped convolution có 32 group convolution. Như 2 kiến trúc trước, ta vẫn có một skip connection từ input cộng với convolution path.

3 kiến trúc block trên là tương đương nhau nên để implement ta thường chọn kiến trúc block (c).

So sánh kiến trúc ResNeXt với ResNet

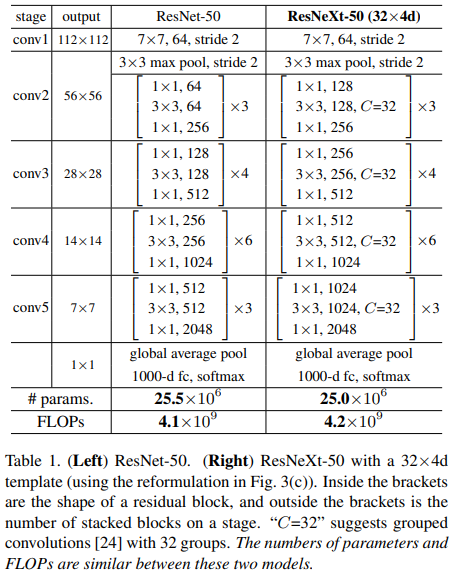
Thông qua bảng trên, ta thấy rằng ResNet-50 chính là một phiên bản đặc biệt của ResNeXt-50 với $C=1$ và $d=64$ . Đặc biệt, lượng tham số và FLOPs của 2 mô hình là gần tương đương nhau.

Model Capacity

Việc chọn giá trị cardinality $C$ và bottleneck width $d$ là rất quan trọng ảnh hưởng tới hiệu suất của mô hình. Như hình trên, block của ResNeXt đang có $C=32$ và $d=4$ . Công thức tính lượng tham số trong 1 block của ResNeXt là:

$C \cdot(256 \cdot d+3 \cdot 3 \cdot d \cdot d+d \cdot 256)$

Với block ResNet bên trái, ta có lượng tham số là $256 · 64 + 3 · 3 · 64 · 64 + 64 · 256 ≈ 70000$ tham số. Trong khi block ResNeXt, nếu chọn $C = 32$ và $d = 4$ ta cũng có lượng tham số gần tương đương. Trong phần thực nghiệm, ta sẽ đánh giá xem $C$ và $d$ ảnh hưởng như nào tới hiệu suất mô hình.

Coding

Model ResNeXt được cài đặt như sau:

import torch
import torch.nn as nn
import torch.nn.functional as F
from collections import OrderedDict

from torch.autograd import Variable

"""
NOTICE:
    BasicBlock_B is not implemented
    BasicBlock_C is recommendation
    The full architecture consist of BasicBlock_A is not implemented.
"""



class ResBottleBlock(nn.Module):
    
    def __init__(self, in_planes, bottleneck_width=4, stride=1, expansion=1):
        super(ResBottleBlock, self).__init__()
        self.conv0=nn.Conv2d(in_planes,bottleneck_width,1,stride=1,bias=False)
        self.bn0 = nn.BatchNorm2d(bottleneck_width)
        self.conv1=nn.Conv2d(bottleneck_width,bottleneck_width,3,stride=stride,padding=1,bias=False)
        self.bn1=nn.BatchNorm2d(bottleneck_width)
        self.conv2=nn.Conv2d(bottleneck_width,expansion*in_planes,1,bias=False)
        self.bn2=nn.BatchNorm2d(expansion*in_planes)
        
        self.shortcut=nn.Sequential()
        if stride!=1 or expansion!=1:
            self.shortcut=nn.Sequential(
                nn.Conv2d(in_planes,in_planes*expansion,1,stride=stride,bias=False)
            )

    def forward(self, x):
        out = F.relu(self.bn0(self.conv0(x)))
        out = F.relu(self.bn1(self.conv1(out)))
        out = self.bn2(self.conv2(out))
        out += self.shortcut(x)
        out = F.relu(out)
        return out


class BasicBlock_A(nn.Module):
    def __init__(self, in_planes, num_paths=32, bottleneck_width=4, expansion=1, stride=1):
        super(BasicBlock_A,self).__init__()
        self.num_paths = num_paths
        for i in range(num_paths):
            setattr(self,'path'+str(i),self._make_path(in_planes,bottleneck_width,stride,expansion))

        # self.paths=self._make_path(in_planes,bottleneck_width,stride,expansion)
        self.conv0=nn.Conv2d(in_planes*expansion,expansion*in_planes,1,stride=1,bias=False)
        self.bn0 = nn.BatchNorm2d(in_planes * expansion)
        
        self.shortcut = nn.Sequential()
        if stride != 1 or expansion != 1:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_planes, in_planes * expansion, 1, stride=stride, bias=False)
            )

    def forward(self, x):
        out = self.path0(x)
        for i in range(1,self.num_paths):
            if hasattr(self,'path'+str(i)):
                out+getattr(self,'path'+str(i))(x)
            # out+=self.paths(x)
            # getattr
        # out = torch.sum(out, dim=1)
        out = self.bn0(out)
        out += self.shortcut(x)
        out = F.relu(out)
        return out

    def _make_path(self, in_planes, bottleneck_width, stride, expansion):
        layers = []
        layers.append(ResBottleBlock(
            in_planes, bottleneck_width, stride, expansion))
        return nn.Sequential(*layers)




class BasicBlock_C(nn.Module):
    """
    increasing cardinality is a more effective way of 
    gaining accuracy than going deeper or wider
    """

    def __init__(self, in_planes, bottleneck_width=4, cardinality=32, stride=1, expansion=2):
        super(BasicBlock_C, self).__init__()
        inner_width = cardinality * bottleneck_width
        self.expansion = expansion
        self.basic = nn.Sequential(OrderedDict(
            [
                ('conv1_0', nn.Conv2d(in_planes, inner_width, 1, stride=1, bias=False)),
                ('bn1', nn.BatchNorm2d(inner_width)),
                ('act0', nn.ReLU()),
                ('conv3_0', nn.Conv2d(inner_width, inner_width, 3, stride=stride, padding=1, groups=cardinality, bias=False)),
                ('bn2', nn.BatchNorm2d(inner_width)),
                ('act1', nn.ReLU()),
                ('conv1_1', nn.Conv2d(inner_width, inner_width * self.expansion, 1, stride=1, bias=False)),
                ('bn3', nn.BatchNorm2d(inner_width * self.expansion))
            ]
        ))
        self.shortcut = nn.Sequential()
        if stride != 1 or in_planes != inner_width * self.expansion:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_planes, inner_width * self.expansion, 1, stride=stride, bias=False)
            )
        self.bn0 = nn.BatchNorm2d(self.expansion * inner_width)

    def forward(self, x):
        out = self.basic(x)
        out += self.shortcut(x)
        out = F.relu(self.bn0(out))
        return out

class ResNeXt(nn.Module):
    def __init__(self, num_blocks, cardinality, bottleneck_width, expansion=2, num_classes=10):
        super(ResNeXt, self).__init__()
        self.cardinality = cardinality
        self.bottleneck_width = bottleneck_width
        self.in_planes = 64
        self.expansion = expansion
        
        self.conv0 = nn.Conv2d(3, self.in_planes, kernel_size=3, stride=1, padding=1)
        self.bn0 = nn.BatchNorm2d(self.in_planes)
        self.pool0 = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        self.layer1=self._make_layer(num_blocks[0],1)
        self.layer2=self._make_layer(num_blocks[1],2)
        self.layer3=self._make_layer(num_blocks[2],2)
        self.layer4=self._make_layer(num_blocks[3],2)
        self.linear = nn.Linear(self.cardinality * self.bottleneck_width, num_classes)

    def forward(self, x):
        out = F.relu(self.bn0(self.conv0(x)))
        # out = self.pool0(out)
        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.layer4(out)
        out = F.avg_pool2d(out, 4)
        out = out.view(out.size(0), -1)
        out = self.linear(out)
        return out

    def _make_layer(self, num_blocks, stride):
        strides = [stride] + [1] * (num_blocks - 1)
        layers = []
        for stride in strides:
            layers.append(BasicBlock_C(self.in_planes, self.bottleneck_width, self.cardinality, stride, self.expansion))
            self.in_planes = self.expansion * self.bottleneck_width * self.cardinality
        self.bottleneck_width *= 2
        return nn.Sequential(*layers)


def resnext26_2x64d():
    return ResNeXt(num_blocks=[2, 2, 2, 2], cardinality=2, bottleneck_width=64)


def resnext26_4x32d():
    return ResNeXt(num_blocks=[2, 2, 2, 2], cardinality=4, bottleneck_width=32)


def resnext26_8x16d():
    return ResNeXt(num_blocks=[2, 2, 2, 2], cardinality=8, bottleneck_width=16)


def resnext26_16x8d():
    return ResNeXt(num_blocks=[2, 2, 2, 2], cardinality=16, bottleneck_width=8)


def resnext26_32x4d():
    return ResNeXt(num_blocks=[2, 2, 2, 2], cardinality=32, bottleneck_width=4)


def resnext26_64x2d():
    return ResNeXt(num_blocks=[2, 2, 2, 2], cardinality=32, bottleneck_width=4)


def resnext50_2x64d():
    return ResNeXt(num_blocks=[3, 4, 6, 3], cardinality=2, bottleneck_width=64)


def resnext50_32x4d():
    return ResNeXt(num_blocks=[3, 4, 6, 3], cardinality=32, bottleneck_width=4)

# def test():
#     net = resnext50_2x64d()
#     # print(net)
#     data = Variable(torch.rand(1, 3, 32, 32))
#     output = net(data)
#     print(output.size())

Thực nghiệm

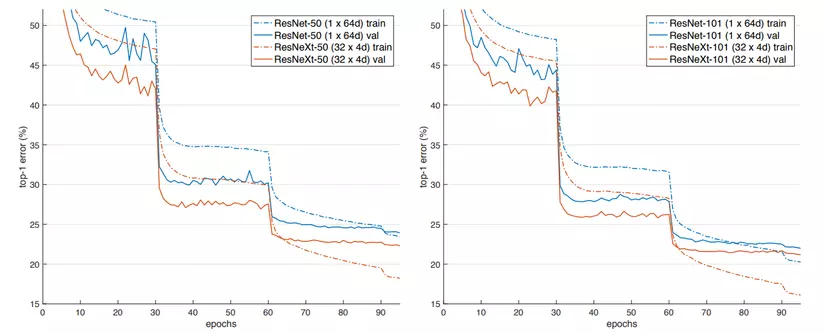
Đồ thị trên biểu diễn Top-1 error của 2 mô hình ResNet và ResNeXt với các setting khác nhau. Nhận thấy rằng, tuy gần tương đương lượng tham số và FLOPs nhưng ResNeXt cho hiệu suất tốt hơn hẳn so với ResNet.

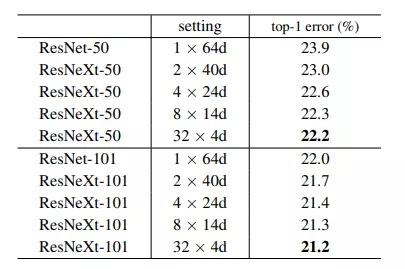
Bảng trên so sánh các kết quả của ResNet và ResNeXt với các setting khác nhau. Nhận thấy với setting 32 x 4d thì ResNeXt có kết quả tốt hơn ResNet (với setting cho lượng tham số và FLOPs tương đương).

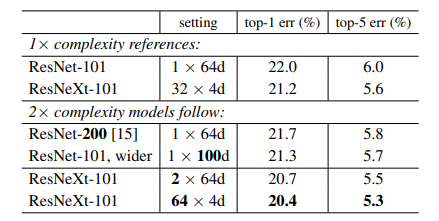
Thông tin trong bảng trên thể hiện khi tăng FLOPs ở cả 2 mô hình với cùng tỉ lệ thì ResNeXt vẫn có hiệu suất tốt hơn ResNet.

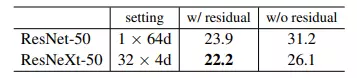
Residual connection đóng vai trò quan trọng ảnh hưởng tới hiệu suất của cả 2 mô hình ResNet và ResNeXt. Việc có residual connection góp phần tăng độ chính xác của mô hình.

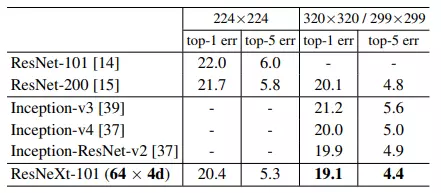
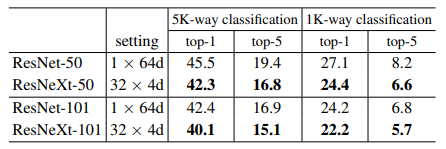
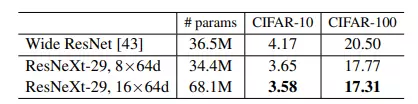
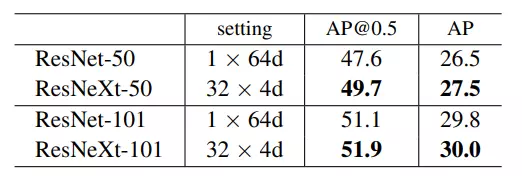
Ở các downstream task (image classification và object detection) với kích thước ảnh đầu vào khác nhau, bộ dữ liệu khác nhau,... ResNeXt vẫn chứng tỏ sự vượt trội thể hiện trong kết quả trình bày ở 4 bảng trên.