Giới thiệu chung

Transformer thể hiện được sức mạnh vượt trội trong nhiều tác vụ AI nói chung và Computer Vision nói riêng, nếu đã là một người học tập và nghiên cứu về AI hẳn bạn không thể không biết để mô hình rất mạnh này . Tuy nhiên, việc áp dụng Transformer vào những hình ảnh có kích thước lớn vẫn tồn tại một số khó khăn về mặt tính toán. Một lý do lớn cho điều này là self-attention tỷ lệ bình phương với số lượng token, tương đương với tỷ lệ bình phương với kích thước hình ảnh. Trên hình ảnh lớn hơn (ví dụ: 1080p), hơn 60% tổng số tính toán trong network chỉ dành cho sử dụng vào việc tạo và áp dụng ma trận attention. Nhóm tác giả đề xuất giải pháp cho vấn đề này đó là Hydra Attention giúp tính toán attention cho Vision Transformers trở nên hiệu quả hơn.

Phương pháp Hydra Attention bắt đầu với một nhận xét có vẻ hơi nghịch lý trong linear attention đó là: Với multihead self-attention tiêu chuẩn, nếu thêm nhiều head vào model thì ta vẫn giữ được lượng tính toán không đổi. Tuy nhiên, sau khi thay đổi thứ tự các thao tác trong linear attention, thêm nhiều head đã thực sự làm giảm chi phí tính toán của layer.

Hydra Attention không chỉ là một công thức tổng quát hơn so với các cách tính toán hiệu quả attention trước đó mà đặc biệt khi sử dụng đúng kernel, nó có thể tăng độ chính xác lên đáng kể.

Trong bài báo nhóm tác giả thực hiện nghiên cứu để xác nhận xem một transformer có thể có bao nhiêu head và họ đã đưa ra 12 là giới hạn cho softmax attention, tuy nhiên khi chọn đúng kernel, bất kì con số nào cũng đều khả thi Nhóm tác giả sử dụng quan sát đó để đề xuất Hydra Attention cho transformer thuần bằng cách tăng số lượng head trong multihead self-attention. Bên cạnh đó, nhóm tác giả cũng phân tích Hydra Attention trên góc nhìn toán học và giới thiệu phương pháp đề visualize sự tập trung của nó. Cuối cùng, nhóm tác giả quan sát rằng bằng cách thay thế các các layer cụ thể bằng Hydra Attention, ta có thể cải thiện độ chính xác lên 1% hoặc khớp với độ chính xác của baseline, đồng thời tạo ra một mô hình nhanh hơn bằng cách sử dụng DeiT-B trên ImageNet -1k.

Hydra Attention

Một multihead self-attention tiêu chuẩn tỷ lệ bình phương với số lượng token trong ảnh. Cụ thể, nếu $T$ là số lượng token và $D$ là số chiều của feature (feature dimension) thì việc tạo và áp dụng attention matrix đều có độ phức tạp $O(T^2D)$. Do đó, điều này đặt ra một vấn đề, khi $T$ lớn (như trường hợp của các hình ảnh lớn) thì thao tác này có thể trở nên không khả thi về mặt tính toán.

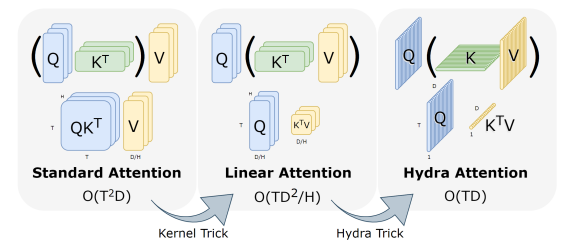
Kernel Trick

Nhiều nghiên cứu trước đây đề xuất giải quyết vấn đề này bằng cách sử dụng "linear" attention. Cho truy vấn $Q$, key $K$ và value $V$ trong $\mathbb{R}^{T \times D}$, softmax self-attention được tính như sau

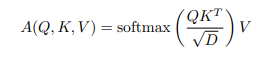
Ta có thể tổng quát phép toán này bằng cách coi softmax(·) như là một pairwise similarity giữa $Q$ và $K$. Ta có thể viết lại như sau

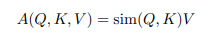
Sau đó, nếu chúng ta chọn một kernel có thể phân rã với biểu diễn đặc trưng $ϕ (·)$ sao cho $sim (x, y) = ϕ (x)ϕ (y)^T$, ta sẽ có

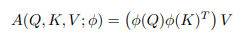
Bằng tính chất kết hợp, ta có thể thay đổi thứ tự tính toán như sau

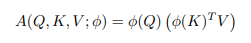
Điều này cho phép ta tính $ϕ(K)^TV$ đầu tiên, thao tác này có độ phức tạp $O(TD^2)$ và tạo một ma trận $D^2$ thay vì $T^2$.

Multi-Head Attention

Mặc dù phép toán đã tuyến tính với $T$, tuy nhiên kết quả vẫn chưa thật sự được như mong muốn: $D$ thường có giá trị lớn ($\ge 768$) và việc tạo một ma trận $D \times D$ và thực hiện một thao tác có độ phức tạp $O(TD^2)$ vẫn khá tốn kém chi phí. Tuy nhiên, ở các công thức trên ta đang mô phỏng cho việc tạo 1 ma trận attention hay 1 "head".

Thực tế, đa phần vision transformer sử dụng $H$ head (thường có giá trị từ 6 tới 16), trong đó mỗi head tạo và áp dụng cho chính ma trận attention của nó. Mỗi head hoạt động trên $D/H$ tập con các feature của chúng từ $Q$, $K$ và $V$. Khi đó ta có phương trình sau

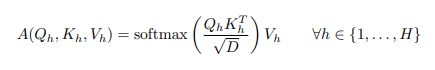
trong đó $Q_h, K_h, V_h ∈ \mathbb{R}^{T × D/H}$. Điều này làm cho tổng số các phép toán không đổi

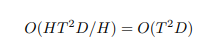
Tuy nhiên, điều này cũng không đúng đối với linear attention. Biến đổi phương trình 4, ta được như sau

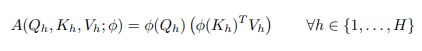
Bằng tính toán attention theo cách này, thêm head thực sự làm giảm số lượng phép tính

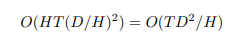
Adding Heads

Từ phương trình trong phần trước, ta thấy rằng khi càng thêm nhiều head và mạng thì multihead linear attention càng nhanh. Điều này dẫn đến một câu hỏi, ta có thể thêm bao nhiêu head là hợp lý. Đa phần transformer sử dụng 6 đến 16 head, phụ thuộc vào số lượng feature $D$, nhưng điều gì xảy ra nếu ta tăng số lượng head lên hơn nữa

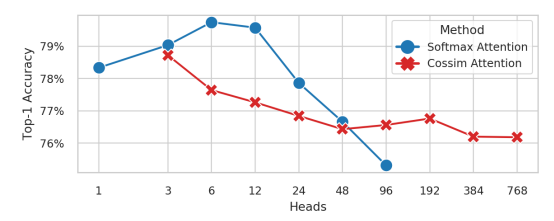
Để tìm hiểu, nhóm tác giả train DeiT-B trên ImageNet-1k và thay đổi số lượng head $H$ sử dụng multi-head self-attention (MSA) tiêu chuẩn với softmax hoặc multi-head linear attention (MLA) với cosin similarity, kết quả thu được trong hình dưới. Về cách sử dụng bộ nhớ, MSA out memory khi $H > 96$ và MLA out memory khi $H <3$.

Về mặt hiệu suất, trong khi MSA với $H > 12$ có độ chính xác giảm sâu, độ chính xác cho MLA với cosin similarity vẫn khá nhất quán cho đến $H = 768$. Thật ngạc nhiên, với lượng head này tức là $H$ đã bằng $D$, nghĩa là mỗi head có chỉ có một scalar feature để làm việc

The Hydra Trick

Như trong hình trên, sẽ là khả thi khi ta scale $H$ lên tùy ý miễn là dùng hàm $sim(x,y)$ (không phải softmax). Để khai thác điều này, nhóm tác giả giới thiệu "thủ thuật hydra" , trong đó đặt $H = D$

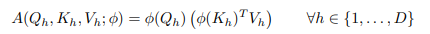
Trong trường hợp này, mỗi $Q_h, K_h, V_h$ là một vector cột trong $\mathbb{R}^{T × 1}$. Nếu vector hóa các phép toán của các head

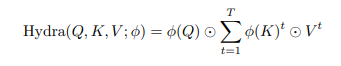
trong đó $⊙$ là element-wise multiplication. Lưu ý rằng có một sự khác biệt nhỏ giữa 2 phương trình này. $\phi$ được áp dụng cho toàn bộ $Q$ và $K$, chứ không phải cho các vectơ cột riêng lẻ $Q_h$ và $K_h$. Điều này rất quan trọng vì đối với mỗi token, $Q_h$ và $K_h$ là các đại lượng vô hướng và việc lấy similarity giữa hai đại lượng vô hướng là rất hạn chế (ví dụ: cosine similarity chỉ có output là -1, 0 hoặc +1).

Để ý một chút ở phương trình trên: Đầu tiên ta có global feature vector $\sum_{t=1}^T \phi(K)^t \odot V^t$ tổng hợp thông tin qua tất cả token trong ảnh. Sau đó mỗi $\phi(Q)$ đánh giá mức độ quan trọng của global feature này với mỗi output token. Do vậy Hydea Attention mix thông tin qua một global bottleneck hơn là mix kiểu token-to-token như self-attention thông thường.

Điều này dẫn đến độ phức tạp

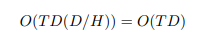
Ta có token mixing module hiệu quả tuyến tính với cả số lượng token và feature trong mô hình và không có hằng số phụ như trong các phương pháp self-attention khác. Lưu ý rằng độ phức tạp về không gian của kỹ thuật này là $O (T D)$, điều này rất quan trọng đối với tốc độ train trong thế giới thực, trong đó nhiều hoạt động bị ràng buộc IO.

Relation to Other Works

Cũng có một số kĩ thuật attention với $O(TD)$ trong bài báo là Attention-Free Transformer (hay AFT-Simple) và PolyNL. Trong phần này ta sẽ tìm hiểu xem Hydra Attention liên quan gì với mỗi mô hình.

AFT-Simple được mô tả như sau

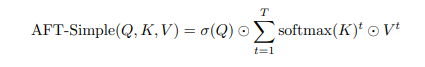
trong đó $σ(·)$ là sigmoid. Nếu ta cho phép $\phi$ thay đổi giữa $Q$ và $K$, thì đây là phép tính toán trực tiếp của phương trinh· trong phần Hydra Trick với $ϕ (Q) = σ (Q)$ và $ϕ (K) = softmax (K)$.

Ngược lại, PolyNL được mô tả như sau

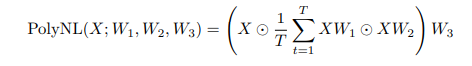
Nếu ta đặt $K = XW_1$, $V = XW_2$ và $ϕ_mean(x) = x/√T$ ta có thể viết

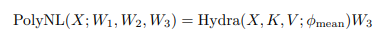
Vì vây, Hydra attention có thể được nhìn theo một form tổng quát hơn so với các phương pháp attention có độ phức tạp $O(TD)$ khác.

Phụ lục

Các kernel khác

Nhóm tác giả liệt kê tất cả các hàm kernel (tức là $ϕ (·)$) đã thử với Hydra Attention. Có ba mối quan tâm chính mà nhóm tác giả gặp phải khi lựa chọn các kernel này. Cụ thể, $ϕ (·)$ phải 1.) không bị giới hạn, 2.) cho phép các giá trị âm, hoặc 3.) là tuyến tính.

Ví dụ, L2 normalization cho cosine similarity ( sử dụng trong bài báo), được giới hạn, cho phép giá trị âm và là tuyến tính. Mặt khác, Sigmoid bị giới hạn, chỉ có giá trị dương và phi tuyến tính.

Từ các thử nghiệm, nhóm tác giả nhận thấy rằng mặc dù hàm được sử dụng cho $Q$ không quan trọng lắm, nhưng $K$ thì có lợi đáng kể khi vừa tuyến tính vừa cho phép nhập các giá trị âm. So với chuẩn hóa L2, softmaxing $K$ làm giảm hiệu suất một cách đáng kể. Trong số các kỹ thuật chuẩn hóa, L2 hoạt động tốt nhất (vượt qua L1 hoặc constant normalization).

Cuối cùng, vì $ϕ (K)$ (khi không phải là softmax) không có tổng bằng 1, nhân nó với $V$ có thể tạo ra cường độ cao hơn mức attention tiêu chuẩn. Vì vậy, nhóm tác giả cho rằng nó có thể hữu ích để chuẩn hóa kết quả của attention layer. Nhóm tác giả kiểm tra hai kernel với “+ LN”, trong đó hoạt động attention được theo sau bởi Layer Norm (trước phép chiếu). Tuy nhiên, điều này dường như không giúp ích được gì, vì vậy tốt hơn là bạn nên để kernel không chuẩn hóa ở đây.

Một số visualizations khác

Nhóm tác giả cung cấp một số hình ảnh visualize cho ta cái nhìn trực quan hơn về tác động của phương pháp. Những hình ảnh này được chọn ngẫu nhiên từ 12 class khác nhau (4 cho mỗi class) từ tập validation ImageNet-1k với tiêu chí lựa chọn duy nhất là hình ảnh phải an toàn để xem . Mô hình dự đoán chính xác hầu hết các hình ảnh này.

Code

Lý thuyết dài vậy nhưng code rất đơn giản

def hydra(q, k, v):
    """
    q, k, and v should all be tensors of shape
    [batch, tokens, features]
    """
    q = q / q.norm(dim=-1, keepdim=True)
    k = k / k.norm(dim=-1, keepdim=True)
    kv = (k * v).sum(dim=-2, keepdim=True)
    out = q * kv
    return out

Tài liệu tham khảo

[1] Hydra Attention: Efficient Attention with Many Heads

[2] The Transformer Family

[3] Attention? Attention!

[4] Katharopoulos, A., Vyas, A., Pappas, N., Fleuret, F.: Transformers are rnns: Fast autoregressive transformers with linear attention. In: ICML (2020)

[5] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L., Polosukhin, I.: Attention is all you need. NeurIPS (2017)

[6] Zhai, S., Talbott, W., Srivastava, N., Huang, C., Goh, H., Zhang, R., Susskind, J.:An attention free transformer. arXiv:2105.14103 [cs.LG] (2021)

[7] Babiloni, F., Marras, I., Kokkinos, F., Deng, J., Chrysos, G., Zafeiriou, S.: Poly-nl: Linear complexity non-local layers with 3rd order polynomials. In: ICCV (2021)