1.6K 89 76

Đã đăng vào Chủ Nhật, 9:00 SA 12 phút đọc

[LLM 101 - Paper reading] Tìm hiểu khả năng suy luận "K-level" trong mô hình ngôn ngữ lớn

Giới thiệu

Các Mô hình Ngôn ngữ Lớn (LLMs) đã mở ra một kỷ nguyên mới trong trí tuệ nhân tạo, giúp cải thiện cách chúng ta giải quyết các vấn đề phức tạp, từ toán học đến những câu hỏi thực tế hàng ngày. Tuy nhiên, việc nghiên cứu về cách LLMs suy nghĩ và đưa ra quyết định một cách linh hoạt trong các tình huống thay đổi liên tục vẫn còn hạn chế.

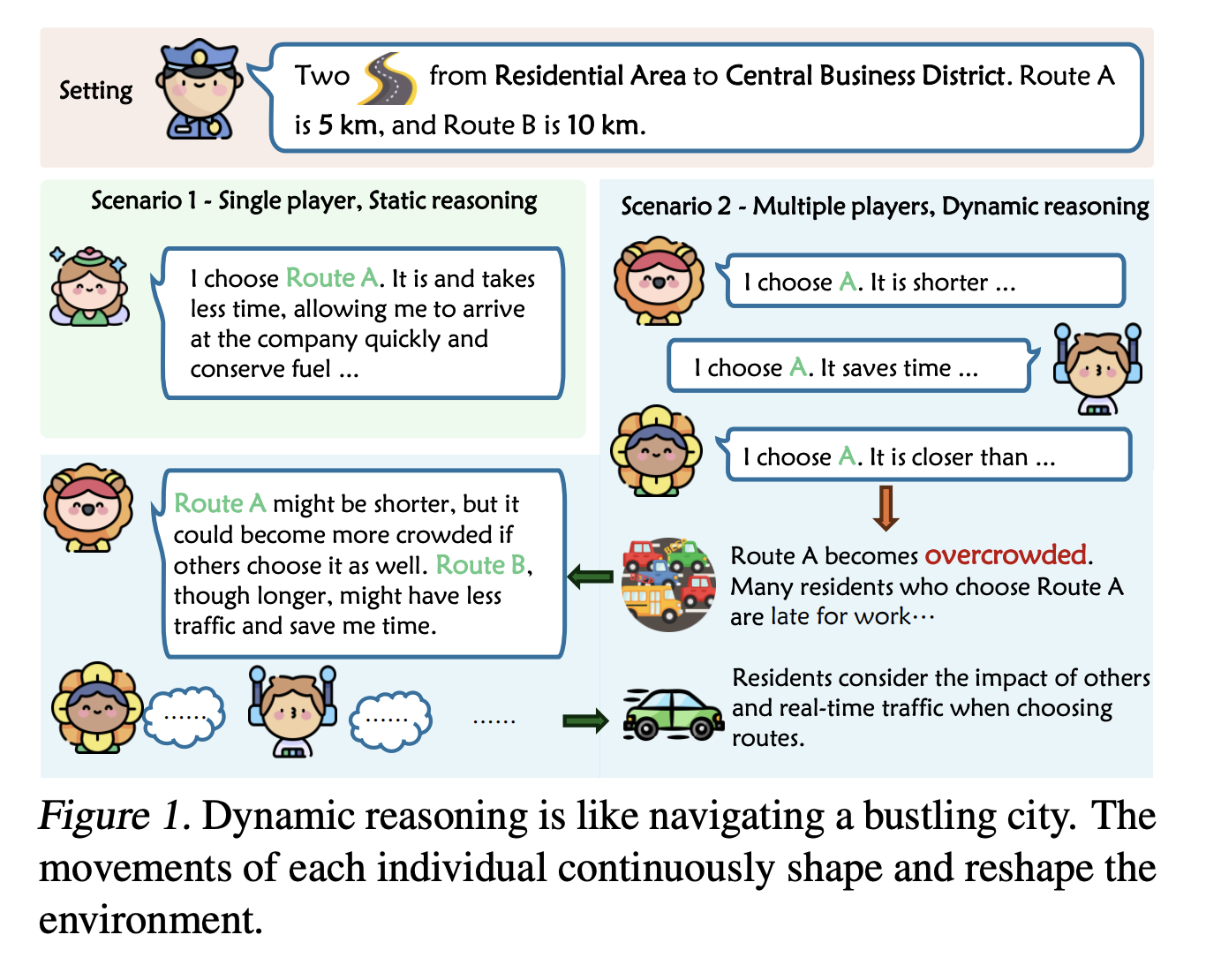
Hãy thử tưởng tượng một ví dụ khi bạn cần di chuyển từ Quận Nam Từ Liêm đến Quận Mỹ Đình (xem hình trên). Giả sử có 2 con đường để đi từ Quận Nam Từ Liêm tới Quận Mỹ Đình tạm gọi là A và B. Đường A dài 7km và đường B dài 8km. Sẽ có 2 trường hợp giả định như sau:

Trường hợp 1: Nếu chỉ có một mình bạn ở Hà Nội. Rất đơn giản thôi, bạn chỉ cần xét các điều kiện có từ ban đầu là "Đường A dài 7km và đường B dài 8km". Vậy, đương nhiên bạn sẽ chọn đường A để đi vì nó ngắn nên tiết kiệm thời gian hơn. Trong trường hợp này, mọi điều kiện đã được xác định cụ thể từ trước và suy luận được đưa ra là tĩnh (static).
Trường hợp 2: Tất nhiên, không phải chỉ có mỗi mình bạn trong tỉnh Hà Nội mà có rất nhiều người trong tỉnh Hà Nội cũng đang muốn di chuyển từ Nam Từ Liêm tới Mỹ Đình. Bạn nhận ra rằng không phải mỗi mình bạn biết là quãng đường A ngắn hơn. Khi mà ai cũng chọn con đường A (vì lý do ngắn hơn) thì con đường này sẽ trở nên đông đúc, tắc nghẽn -> cần nhiều thời gian để đi hơn. Biết được điều này, bạn sẽ có thể không chọn đường A nữa mà sẽ chuyển sang đường B, mặc dù dài hơn một chút nhưng đường thông thoáng, di chuyển sẽ nhanh hơn. Trong trường hợp này, thay vì chỉ xét trên một điều kiện ban đầu là đường A ngắn hơn đường B, mà bạn còn phải suy xét xem những người khác cùng muốn đi từ Nam Từ Liêm tới Mỹ Đình giống mình sẽ di chuyển như nào, mà điều kiện số hai này luôn bất định. Vậy, lựa chọn của bạn và mọi người có sự tương tác với nhau, thậm chí có thể ảnh hưởng lẫn nhau. Môi trường trở nên động (dynamic) và thay đổi liên tục, đòi hỏi các bên tham gia phải thay đổi chiến lược của họ theo thời gian thực. Các tình huống suy luận động như vậy thường gặp trong thế giới thực, ví dụ như phân tích chiến lược kinh doanh, dự đoán thị trường chứng khoán,...

Quay lại vấn đề về LLM, Việc để cho model có thể đưa ra quyết định hoặc câu trả lời chính xác trong một môi trường động như vậy là một thách thức. Bài báo hôm nay chúng ta tìm hiểu đã đề xuất một phương pháp suy luận có tên "K-level Reasoning". Phương pháp này áp dụng tư duy K-level bằng cách lấy "góc nhìn" của đối thủ vào quá trình đưa ra quyết định.

Quá trình suy luận đệ quy này giúp hiểu sâu hơn về bối cảnh chiến lược và cho phép các LLMs đưa ra quyết định thông minh hơn bằng cách tính đến phản ứng có khả năng xảy ra của đối thủ, từ đó đạt được kết quả tốt hơn trong các thử nghiệm so với phương pháp suy luận truyền thống.

Đặt vấn đề

Dynamic Reasoning trong LLM

Trong một môi trường động, mỗi cá nhân liên tục điều chỉnh chiến lược của mình dựa trên môi trường xung quanh và hành động của người khác. Quá trình này tạo ra một chuỗi phức tạp giữa hành động và phản ứng, nơi mỗi quyết định không chỉ ảnh hưởng đến hiện tại mà còn định hình tương lai.

Để mô tả quá trình này một cách toán học, chúng ta bắt đầu từ điểm khởi đầu được gọi là $E_0$ , đại diện cho trạng thái ban đầu của môi trường. Khi thời gian trôi qua, môi trường tiến triển thành $E_{t+1}$ dựa trên quyết định của mọi người tại thời điểm $t$ , ký hiệu là $d_{t}^i$ , với $i$ đại diện cho mỗi cá nhân.

Sự chuyển đổi này có thể được biểu diễn qua công thức:

$E_{t+1} = \text{Transfer}(E_t, D_t)$

trong đó, $D_t$ là tập hợp các quyết định của tất cả cá nhân tại thời điểm $t$ và $\text{Transfer}$ là hàm biểu thị cách môi trường thay đổi dựa trên những quyết định đó.

Để đưa ra quyết định tối ưu $d_{t+1}^i$ cho bước tiếp theo, mỗi cá nhân cần phải xem xét không chỉ trạng thái môi trường hiện tại $E_{t+1}$ mà còn cả hành động trong quá khứ và dự đoán về tương lai của người khác. Điều này đòi hỏi một cách tiếp cận linh hoạt, hiểu được cả bản chất động của môi trường và sự tương tác giữa các cá nhân.

Pilot task

Nhóm tác giả đã nghiên cứu khả năng suy luận động của LLMs thông qua hai trò chơi sau:

Đoán 0.8 của Trung bình (GUESSING 0.8 OF THE AVERAGE - G0.8A): Trong trò chơi này, mỗi người chơi chọn một số từ 1 đến 100 và mục tiêu là chọn số gần nhất với 80% của trung bình tổng các số mà mọi người chọn. Điều này kiểm tra khả năng dự đoán của người chơi về suy nghĩ của người khác.
Trò chơi Đấu giá Sinh tồn (SURVIVAL AUCTION GAME - SAG): Đặt trong bối cảnh một thị trấn hạn hán, mục tiêu là sống sót qua 10 ngày bằng cách đấu giá nguồn nước để giữ cho điểm sức khỏe luôn trên 0. Trò chơi này kiểm tra khả năng quản lý nguồn lực và dự đoán hành động cạnh tranh của người chơi.

Cả hai trò chơi đều kiểm tra khả năng suy luận động của LLMs trong việc dự đoán và thích ứng với hành động của người khác trong một môi trường liên tục thay đổi.

Metrics

Để đo lường khả năng suy luận động của LLMs, nhóm tác giả thiết lập một hệ thống đánh giá toàn diện bao gồm 4 chỉ số. Với các nhiệm vụ được định nghĩa rõ ràng:

Tỷ Lệ Thắng (Win Rate):

$\text{WinRate} = \frac{\text{Số Lần Thắng}}{\text{Tổng Số Vòng Trò Chơi Mỗi Thử Nghiệm} \times \text{Số Lần Thử Nghiệm}}$

Tỷ lệ Thắng được tính dựa trên số lần thắng chia cho tổng số vòng trò chơi, cung cấp một thước đo cho khả năng tổng thể. Trong các trò chơi như G0.8A, Tỷ Lệ Thắng là một chỉ số quan trọng.

Vòng Sống Sót Trung Bình (Average Survival Round):

$\text{AvgSurvivalRound} = \frac{\text{Vòng Sống Sót Trong Mỗi Thử Nghiệm}}{\text{Số Lần Thử Nghiệm}}$

Chỉ số này tính toán số vòng trung bình mà người chơi còn "tồn tại" trong trò chơi. Đây là cách hiệu quả để đánh giá hiệu suất trong trò chơi dựa trên loại trừ, như SAG.

Chỉ Số Thích Nghi (Adaptation Index):

$\text{Adaptation Index} = \frac{\text{Sai Lệch Mục Tiêu Ở Nửa Sau}}{\text{Sai Lệch Mục Tiêu Ở Nửa Đầu}}$

Chỉ số này đánh giá khả năng thích nghi và cải thiện hiệu suất của người chơi theo thời gian, được xác định bằng cách so sánh sự sai lệch từ chiến lược tối ưu trong nửa đầu của các vòng đấu với nửa sau.

Độ Chính Xác Dự Đoán (Prediction Accuracy):

Trong G0.8A:

$\text{Pred Acc} = \frac{\sum |\text{AvgPred} - \text{AvgActual}|}{\text{Số Lần Thử Nghiệm}}$

Trong SAG:

$\text{Pred Acc} = \frac{\sum |\text{MaxBidPred} - \text{MaxBidActual}|}{\text{Số Lần Thử Nghiệm}}$

Chỉ số này đánh giá độ chính xác của dự đoán của người chơi về các động thái tương lai của đối thủ. Trong G0.8A, nó liên quan đến việc tính toán sự chênh lệch tuyệt đối giữa dự đoán trung bình của người chơi và trung bình thực tế trong mỗi vòng. Trong SAG, trọng tâm chuyển sang đo lường sai số tuyệt đối giữa dự đoán của người chơi về giá thầu cao nhất của đối thủ và giá thầu cao nhất thực sự do họ đưa ra.

K-Level Reasoning

Lý thuyết phân cấp nhận thức, được Stahl giới thiệu năm 1993, giải thích cách mọi người đưa ra quyết định trong các tình huống cạnh tranh và tương tác. Theo lý thuyết này, mọi người xếp mình và người khác vào các "cấp độ suy nghĩ" khác nhau.

Người ở cấp độ đầu tiên chỉ phản ứng với môi trường mà không quan tâm đến hành động của người khác. Còn những người ở cấp độ cao hơn sẽ đưa ra quyết định dựa trên những gì họ nghĩ người chơi cấp độ thấp hơn sẽ làm.

Nhóm tác giả sử dụng ý tưởng này để phát triển "K-Level Reasoning" cho LLMs, giúp chúng mô phỏng và dự đoán hành vi của đối thủ. Phương pháp này mô tả qua hai bước:

Điều kiện ban đầu được đặt là $d^{t,1} = f(E_t)$ , trong đó $d^{t,1}$ là quyết định ở thời điểm $t$ với suy nghĩ ở cấp độ 1 và $E_t$ là trạng thái môi trường tại thời điểm đó.
Công thức đệ quy được biểu diễn là $d^{t,k} = f(E_t, \hat{d}^{t,k-1}_1, ..., \hat{d}^{t,k-1}_n)$ , trong đó $d^{t,k}$ là quyết định tại thời điểm $t$ với suy nghĩ ở cấp độ $k$ , và $\hat{d}^{t,k-1}_1, ..., \hat{d}^{t,k-1}_n$ là dự đoán quyết định của các người chơi khác ở cấp độ suy luận $k-1$ .

Phương pháp này giúp LLMs hiểu sâu hơn về các tình huống động, qua đó thích nghi và phản ứng hiệu quả hơn với hành vi của đối thủ. Tuy nhiên, cần lưu ý rằng "overthinking" có thể không mang lại lợi ích và thậm chí dẫn đến những quyết định sai lầm . Đôi khi, chỉ cần hiểu đối thủ một cách vừa phải là đủ để đưa ra quyết định tối ưu.

Thực nghiệm

Chi tiết về setting thực nghiệm và kết quả các bạn có thể đọc trong paper K-Level Reasoning with Large Language Models

Kết luận

Bài báo đề xuất một chiến thuật prompting mới để cải thiện độ hiệu quả của LLMs trong các tình huống động mà việc đưa ra quyết định phụ thuộc vào nhiều bên theo thời gian thực. Dựa vào ý tưởng của bài báo các bạn có thể áp dụng vào để giải quyết các bài toán cụ thể của mình.

Tài liệu tham khảo

[1] K-Level Reasoning with Large Language Models

LLM