1.6K 86 72

Đã đăng vào thg 10 21, 4:00 SA 15 phút đọc

LLM 101 | FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

Đóng góp của bài báo

Nếu quen thuộc với Self-attention thì chúng ta đều biết rằng Self-attention có độ phức tạp bậc 2 với độ dài của chuỗi đầu vào. Điều đó có nghĩa là Transformer sẽ chạy rất chậm và tiêu tốn bộ nhớ với các chuỗi dài. Hạn chế lớn này của Transformer sẽ ảnh hưởng đến rất nhiều tới mô hình ngôn ngữ lớn, khi đầu vào là các context, chuỗi văn bản dài. Câu hỏi quan trọng đặt ra là làm như nào để cho attention nhanh hơn, sử dụng ít bộ nhớ hơn?

Trước đây cũng có nhiều các phương pháp xấp xỉ attention được đề xuất giúp giảm độ phức tạp tính toán và bộ nhớ của attention. Một số ý tưởng được đề xuất là sparse-approximation, low-rank approximation và các cách kết hợp của chúng. Mặc dù các phương pháp này làm giảm lượng tính toán xuống linear hoặc gần linear với độ dài chuỗi đầu vào nhưng đa phần khi chạy thực tế thì tốc độ không vượt attention tiêu chuẩn và do đó không được áp dụng rộng rãi. Một nguyên nhân chính là do các phương pháp này tập trung vào việc giảm FLOP mà không chú ý đến chi phí từ việc truy cập bộ nhớ (IO).

Kiến thức cơ bản

Để hiểu được các concept trong paper, ta cần nắm được một số khái niệm dưới đây.

Hiệu suất phần cứng

Trong phần này, ta sẽ tập trung vào GPU, là thiết bị phần cứng thường xuyên được sử dụng trong AI.

Cấu trúc bộ nhớ của GPU.

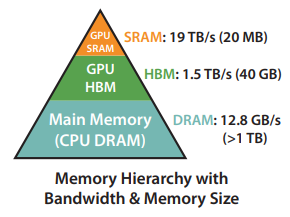
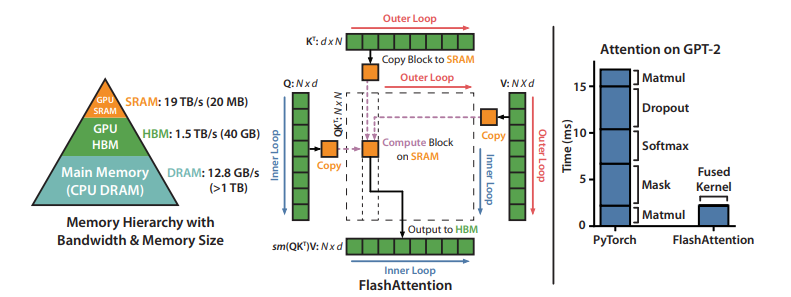
Ta có thể tưởng tượng về bộ nhớ trong GPU là các loại hộp lưu trữ. Ở trong GPU có nhiều loại hộp lưu trữ với tốc độ và dung lượng khác nhau.

High Bandwidth Memory (HBM): Đây là loại hộp lưu trữ lớn, có thể chứa từ 40 đến 80GB dữ liệu. Nó cung cấp băng thông cao từ 1.5 đến 2.0TB/s, điều này có nghĩa là nó có thể truyền dữ liệu nhanh chóng.
On-Chip SRAM: Đây cũng là một loại hộp lưu trữ, nhưng nhỏ hơn nhiều so với HBM. Mỗi bộ xử lý đa luồng trong GPU có khoảng 192KB của SRAM. Điều đặc biệt là SRAM này rất nhanh, với băng thông ước tính khoảng 19TB/s.

Tưởng tượng rằng bạn có một hộp lớn để đựng nhiều đồ và một hộp nhỏ hơn chứa ít đồ hơn, nhưng bạn có thể lấy đồ ra khỏi hộp nhỏ này rất nhanh.

Khi tốc độ tính toán nhanh hơn so với tốc độ của bộ nhớ, việc truy cập dữ liệu từ bộ nhớ trở thành bottleneck. Lý do là việc tính toán phải chờ dữ liệu từ bộ nhớ và do đó làm giảm hiệu suất chung.

Để giải quyết vấn đề này, việc tận dụng bộ nhớ nhanh SRAM trở nên quan trọng. Bằng cách sử dụng SRAM này hiệu quả hơn, ta có thể tránh được sự phụ thuộc quá mức vào bộ nhớ chậm (HBM), từ đó cải thiện hiệu suất tổng thể của quá trình tính toán.

Execution Model. Mô hình thực thi (Execution Model) trên GPU là quá trình thực hiện các phép tính thông qua một lượng lớn các luồng (threads) để thực hiện một hoạt động cụ thể được gọi là một "kernel".

Mỗi kernel sẽ tải dữ liệu input từ bộ nhớ chính (HBM - High Bandwidth Memory) vào các thanh ghi (registers) và SRAM. Sau đó, việc tính toán được thực hiện trên dữ liệu trong các thanh ghi và SRAM. Kết quả tính toán sau đó được ghi lại vào HBM. Điều này giống như việc lấy sách từ kệ, đọc và viết ghi chú, rồi đặt lại sách vào kệ.

Hiệu suất. Hiệu suất của các hoạt động trên GPU phụ thuộc vào việc chúng sử dụng nhiều lần tính toán hay nhiều lần truy cập bộ nhớ hơn. Sự phụ thuộc này được tính bằng arithmetic intensity, là tỉ lệ giữa số lượng phép tính trên mỗi byte dữ liệu cần truy cập trong bộ nhớ. Ta chia thành hai loại chính:

Tập trung vào tính toán (Compute-bound): Thời gian thực hiện chủ yếu phụ thuộc vào số lượng phép tính được thực hiện, trong khi thời gian truy cập HBM ít hơn nhiều. Ví dụ điển hình là phép nhân ma trận với kích thước lớn và tính tích chập với số lượng channel lớn.
Tập trung vào bộ nhớ (Memory-bound): Thời gian thực hiện phụ thuộc chủ yếu vào số lần truy cập bộ nhớ, trong khi thời gian tính toán ít hơn. Ví dụ như phép tính trên từng phần tử (activation, dropout) và các phép tính reduction (sum, softmax, batch norm, layer norm).

Kernel fusion. Cách tiếp cận phổ biến nhất để tăng tốc hoạt động thuộc loại Memory-bound GPU là "kernel fusion". Nếu có nhiều phép tính được áp dụng cho cùng một dữ liệu đầu vào thì dữ liệu đó chỉ cần được tải một lần từ HBM, thay vì nhiều lần cho mỗi phép tính. Các trình biên dịch có thể tự động hợp nhất nhiều phép tính thực hiện trên từng phần tử dữ liệu (elementwise operations).

Tuy nhiên, trong ngữ cảnh của việc huấn luyện mô hình, các giá trị trung gian vẫn cần được ghi lại vào HBM để lưu trữ cho quá trình lan truyền ngược (backward pass), điều này giảm hiệu quả của kernel fusion. Điều này có nghĩa là, mặc dù chúng ta có thể tối ưu hoá bằng cách gộp nhiều phép tính lại với nhau để giảm số lần truy cập bộ nhớ, nhưng trong quá trình huấn luyện mô hình, việc lưu trữ các giá trị trung gian vẫn đòi hỏi ghi lại vào HBM, làm giảm hiệu quả của cách tối ưu đó.

Attention

Chúng ta đều biết rằng việc tính toán ma trận Attention được thực hiện từ 3 ma trận $\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d}$ , trong đó $N$ là độ dài chuỗi và $d$ là head dimension.

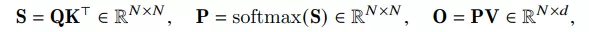
Nhận thấy rằng, ta cần lưu 2 ma trận $\mathbf{S}$ và $\mathbf{P}$ vào HBM để thực hiện các lần tính toán sau, khi đó độ phức tạp bộ nhớ là $O(N^2)$ . Mặt khác, các hoạt động tính toán ma trận Attention chủ yếu là memory-bound (ví dụ như softmax), cho nên việc truy cập từ bộ nhớ nhiều lần sẽ làm giảm tốc độ tính toán tổng thể. Cụ thể hơn, bạn có thể xem thuật toán bên dưới:

FlashAttention

Bài toán đặt ra là làm sao để tính toán chính xác kết quả ma trận attention mà thực hiện ít lần đọc/ghi vào HBM và hạn chế lưu tạm các ma trận lớn cho quá trình lan truyền ngược (backward pass).

Thuật toán

Ta phát biểu lại bài toán như sau: Cho các input $\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d}$ trong HBM, mục tiêu là tính ma trận attention đầu ra $\mathbf{O} \in \mathbb{R}^{N \times d}$ và lưu vào HBM sao cho số lần truy cập HBM là ít nhất.

Ta có 2 kĩ thuật để giải quyết bài toán này là Tiling và Recomputation.

Tiling (sử dụng trong cả quá trình forward và backward). Ý tưởng là ta sẽ chia $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ thành các block, sau đó load các block này từ HBM và SRAM. Điều này giúp ta tận dụng được tốc độ của SRAM bằng cách tách nhỏ ma trận đầu vào.

Khi đó softmax của vector $x \in \mathbb{R}^B$ được tính như sau:

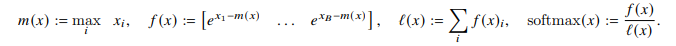
Cụ thể với 2 vector riêng biệt, paper đã trình bày cách tính softmax của concat của 2 vector này như sau:

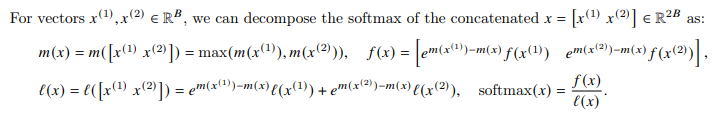
Ta có 2 đại lượng mới là $m(x)$ và $l(x)$ , bằng cách lưu lại các đại lượng này thì việc tính toán softmax cho 1 block chỉ cần thực hiện trong đúng 1 lần.

Recomputation (chỉ dùng trong quá trình backward). Một trong những mục tiêu của chúng ta là không lưu giá trị tạm tới mức $O(N^2)$ trong quá trình lan truyền ngược Theo cách làm cũ, ta cần phải lưu ma trận $\mathbf{S}, \mathbf{P}$ vào HBM để tính gradient. Tuy nhiên, trong cách mới, ta chỉ cần lưu output $\mathbf{O}$ và cặp $(m, l)$ là có thể tính toán ma trận $\mathbf{S}, \mathbf{P}$ một cách đơn giản ở trong SRAM. Dễ thấy, cách này làm tăng FLOPs lên nhưng do số lần truy cập HBM giảm đáng kể nên bản chất tốc độ của cả quá trình vẫn nhanh hơn nhiều so với cách làm cũ.

Cuối cùng, ta có mã giả thuật toán như sau:

Ta cùng đi vào từng bước của thuật toán

Dòng 1: Tính block size. Giả sử $M = 2000, d = 64$ , ta có $B_c = 8$ . Vậy tức là mỗi lần ta sẽ lấy 1 block gồm 8 vector $k$ và 8 vector $v$ để tính toán, tương tự với $q$ .
Dòng 2: Khởi tạo giá trị ban đầu cho $\mathbf{O}, l, m$ .
Dòng 3: Chia $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ thành các block với block size được tính từ bước 1.
Dòng 4: Chia $\mathbf{O}, l, m$ thành các block với block size giống $\mathbf{Q}$ .
Dòng 5: Thực hiện lặp qua các cột, tức là các cặp key/value.
Dòng 6: Load $\mathbf{K}_j, \mathbf{V}_j$ từ HBM vào SRAM. Vì block size ta tính bằng cách chia $M$ cho $4d$ nên ta vẫn còn 50% SRAM để lưu $\mathbf{Q}$ và $\mathbf{O}$ .
Dòng 7: Thực hiện lặp qua các query vector.
Dòng 8: Tiếp tục load các giá trị từ HBM và SRAM.
Dòng 9: Tính giá trị $\mathbf{S}_{ij}$ . Để ý rằng ở đây ta không còn giá trị $\mathbf{S}$ như attention tiêu chuẩn mà chỉ có "1 phần" của nó.
Dòng 10: Tính $\tilde{m}_{ij}, \tilde{\mathbf{P}}_{ij}, \tilde{l}_{ij}$
Dòng 11: Cập nhật $m^{new}_i$ và $l^{new}_i$ mới.
Dòng 12: Tính toán giá trị $\mathbf{O}_i$ và lưu vào HBM
Dòng 13: Gán giá trị $m_i = m^{new}_i$ và $l_i = l^{new}_i$ và lưu vào HBM.

Với thuật toán này ta có $O(N^2d)$ FLOP nhưng chỉ yêu cầu $O(N)$ về bộ nhớ.

IO Complexity của FlashAttention

Trong phần này, nhóm tác giả phát biểu một định lý sau:

Gọi $N$ là độ dài chuỗi, $d$ là head dimension và $M$ là kích thước của SRAM với $d \le M \le Nd$ . Cách tính ma trận attention tiêu chuẩn yêu cầu $O(Nd + N^2)$ lần truy cập HBM. Trong khi đó FlashAttention chỉ yêu cầu $O(N^2d^2M^{-1})$ lần truy cập HBM.

Thường thì $d$ sẽ có giá trị $(64-128)$ và $M$ có kích thước 100KB, $d^2$ nhỏ hơn rất nhiều lần so với $M$ . Do đó, FlashAttention yêu cầu ít truy cập HBM hơn nhiều lần so với việc sử dụng phương pháp tiêu chuẩn. Điều này dẫn đến thời gian thực thi nhanh hơn.

Ngoài ra, ta cũng có một mệnh đề sau:

Gọi $N$ là độ dài chuỗi, $d$ là head dimension và $M$ là kích thước của SRAM với $d \le M \le Nd$ . Ta nói rằng, không tồn tại một thuật toán có thể tính chính xác attention với $O(N^2d^2M^{-1})$ lần truy cập HBM cho mọi $M$ nằm trong đoạn $[d, Nd]$ .

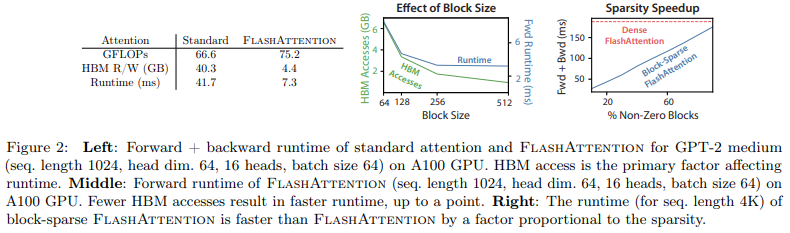
Như đã trình bày ở trên, ở FlashAttention mặc dù lượng FLOP tăng nhưng runtime lại giảm đi rất nhiều do số lần truy cập HBM giảm đi đáng kể.

Ngoài ra, runtime còn phụ thuộc vào block size $B_c$ của FlashAttention. Khi block size tăng, số lần truy cập HBM giảm và runtime cũng giảm. Với block size lớn (trên 256), runtime sẽ bị bottleneck bởi các yếu tốt khác (ví dụ như arithmetic operations). Mặt khác, block size càng lớn sẽ không fit với SRAM có size nhỏ.

Block-Sparse FlashAttention

Block-Sparse FlashAttention là phiên bản mở rộng của FlashAttention, đây là một cách để xấp xỉ attention với độ phức tạp IO nhỏ hơn FlashAttention và do đó có tốc độ nhanh hơn khoảng 2-4 lần.

Ý tưởng ở đây là ta sử dụng một ma trận mask để bỏ qua một số lần truy cập trong vòng for lồng ở thuật toán trên và từ đó có tốc độ chạy nhanh hơn tỉ lệ với hệ số thưa thớt (sparsity coefficient).

Ta có mệnh đề sau: Gọi $N$ là độ dài chuỗi, $d$ là head dimension và $M$ là kích thước của SRAM với $d \le M \le Nd$ . Ta có Block-sparse FlashAttention yêu cầu $O(Nd + N^2d^2M^{-1}s)$ lần truy cập HBM, trong đó $s$ là tỉ lệ nonzero block trong block-sparsity mask.

Cho một chuỗi có độ dài $N$ , $s$ thường được đặt bằng $N^{-1/2}$ hoặc $N^{-1}logN$ , kết quả là ta có độ phức tạp IO tương ứng là $O(N\sqrt{N})$ hoặc $O(N\log N)$ .

Thực nghiệm

Sử dụng FlashAttention cải thiện đáng kể thời gian training của các model NLP (BERT, GPT-2). Kết quả thể hiện trong 2 bảng dưới:

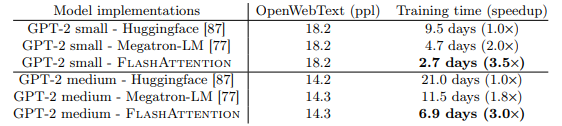
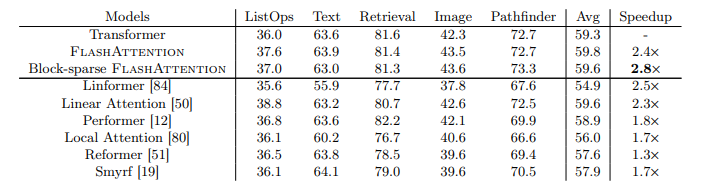
Nhóm tác giả cũng so sánh với các biến thể Transformer khác, FlashAttention và Block-sparse FlashAttention đạt được tốc độ training ấn tượng. Nhóm tác giả thực hiện đo lường độ chính xác, hiệu suất và thời gian huấn luyện của tất cả các mô hình. Mỗi nhiệm vụ có độ dài chuỗi khác nhau dao động từ 1024 đến 4096. Bảng dưới cho thấy rằng FlashAttention đạt được tốc độ bằng 2.4 lần so với attention tiêu chuẩn. Bên cạnh đó, Block-sparse FlashAttention cũng nhanh hơn so với tất cả các phương pháp xấp xỉ attention có trong thực nghiệm.