Cơ bản về vector
Bài đăng này đã không được cập nhật trong 5 năm
1. Định nghĩa
- Vectơ là một đoạn thẳng có hướng. Kí hiệu vectơ có điểm đầu A, điểm cuối B là
- Giá của vectơ là đường thẳng chứa vectơ đó.
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ, kí hiệu .
- Hai vectơ đgl cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.
- Hai vectơ đgl bằng nhau nếu chúng cùng hướng và có cùng độ dài.
Chú ý: + Ta còn sử dụng kí hiệu để biểu diễn vectơ.
+ Qui ước: Vectơ cùng phương, cùng hướng với mọi vectơ.
Mọi vectơ đều bằng nhau.
Hệ thức trung điểm đoạn thẳng: M là trung điểm của đoạn thẳng (O tuỳ ý).
2. Các biểu thức cơ bản của vector
- Phép cộng :
- Phếp trừ :
- Phép nhân scalar :
2.1 Các hình thức khác nhau của vector
- Mẫu thành phần .
- Vector đơn vị: .
- Độ lớn và phương hướng: .
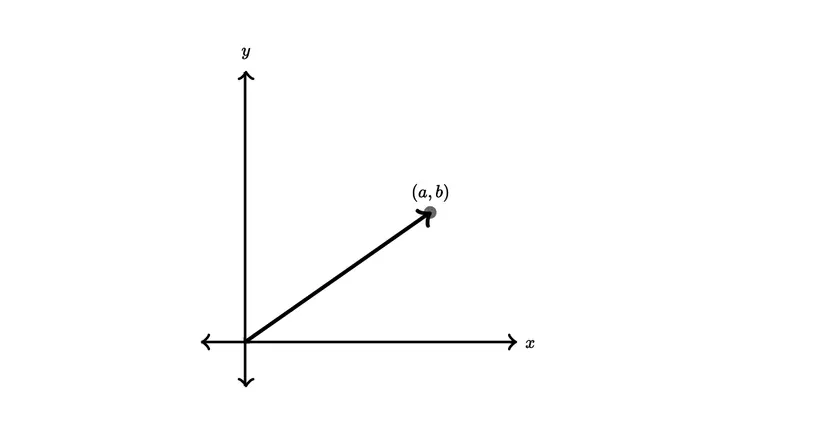
2.1.1 Mẫu thành phần
Ở dạng thành phần, chúng ta coi vectơ là một điểm trên mặt phẳng tọa độ hoặc là một đoạn đường có hướng trên mặt phẳng. Các thành phần là tọa độ x và y của vectơ.
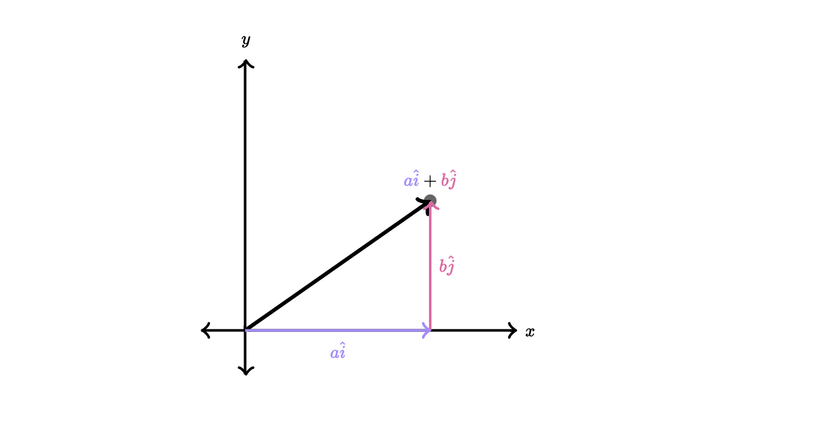
2.1.2 Vector đơn vị
Đây là vector đơn vị ở dạng thành phần của chúng.
Chúng ta có thể bất kỳ vector nào dưới dạng các vector thành phần. ví dụ có thể viết thành
2.1.3 Độ lớn và phương hướng
Xem xét đồ hoạ vector chúng ta có thể biểu diễn chúng dựa trên hướng và độ lớn (góc được tạo từ đường thằng giao vs trục Ox)
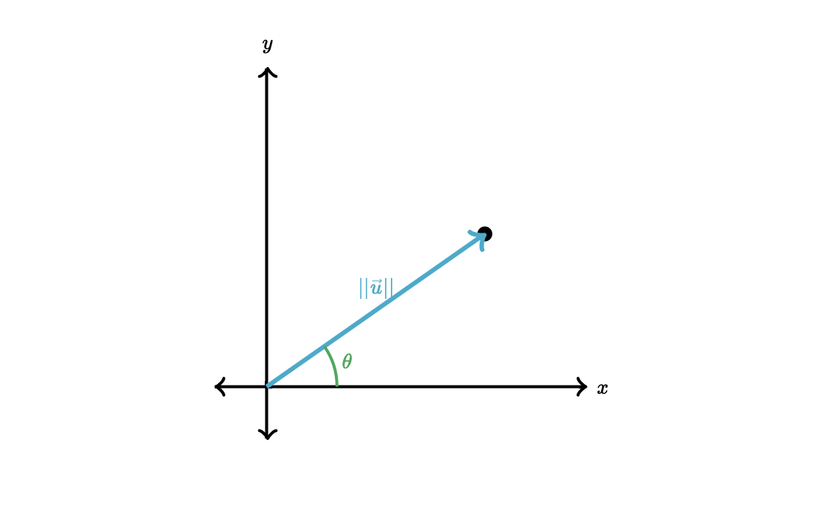
3. Vector độ lơn và hướng
- Độ lớn của br
- Hướng của
- Độ lớn là vector và hướng là :
4. Tài liệu tham khảo
https://www.khanacademy.org/math/precalculus/vectors-precalc
All rights reserved